Python Programming

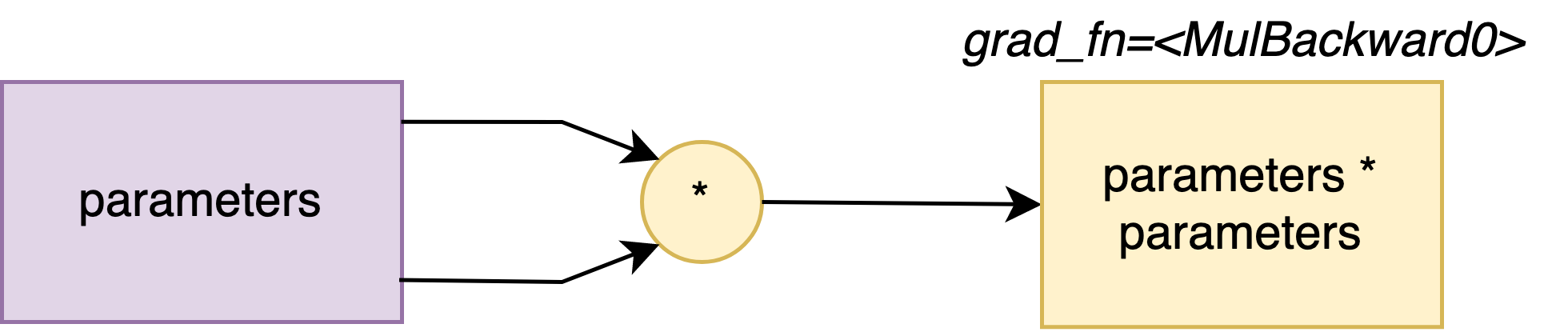
Let’s consider (once again ^^) the squared function $L(\theta) = \theta^2$, and we would like to calculate the gradient $\dfrac{\partial L}{\partial \theta}(\theta_0)$, where $\theta_0 = 1$.

import torch

tensor_0 = torch.Tensor([1])
theta_0 = torch.nn.Parameter(tensor_0)

loss = theta_0 * theta_0
print(loss)

tensor([1.], grad_fn=<MulBackward0>)

print(theta_0.grad)

None

Calculating the gradient of the loss

As said before, we would like to calculate the gradient of the loss $L(\cdot)$ with respect to $\theta$, and evaluate that value at $\theta_0 = 1$: $\dfrac{\partial L}{\partial \theta}(\theta_0)$.

To do so, we simply need to add the following line:

loss.backward()

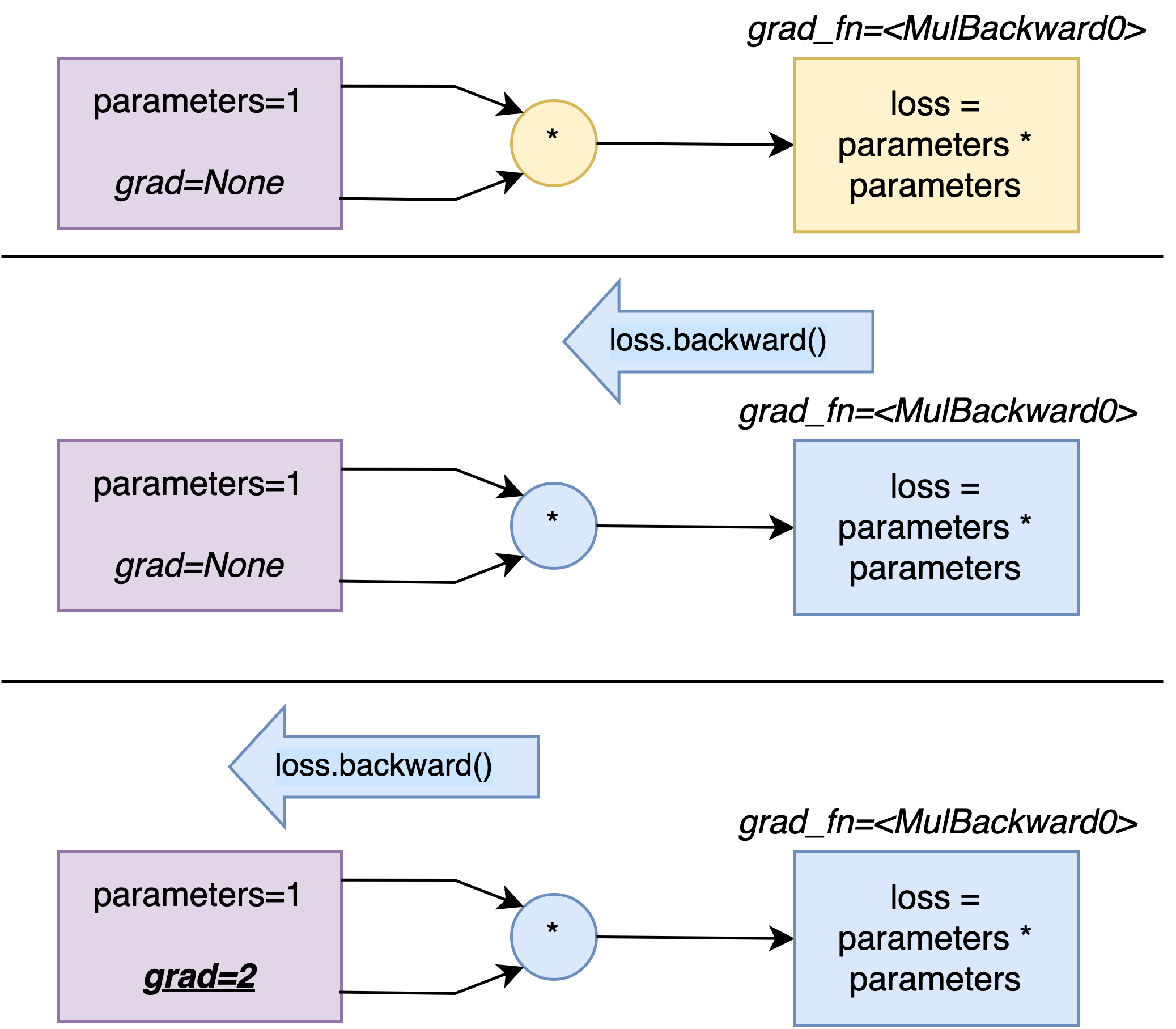
And now if we try to print out theta_0.grad, we get:

tensor([2.])

which corresponds to the value of $\dfrac{\partial L}{\partial \theta}(\theta_0) = 2\theta_0$ (where $\theta_0 = 1$) .

In other words, now we can compute gradients automatically!