Introduction to Deep Learning with PyTorch
Chapter 5: Training a Linear Model with PyTorch
Summary: Final Code and Results
Let’s have a look at our final code, and at the results it produces
Implementation of ModelNumberQuestions
import torch
class ModelNumberQuestions(torch.nn.Module):
def __init__(self):
super().__init__()
self.linear = torch.nn.Linear(in_features=1, out_features=1)
def forward(self, tensor_number_tasks):
return self.linear(tensor_number_tasks)
train_parameters_linear_regression_
def train_parameters_linear_regression(tensor_number_tasks,
tensor_number_questions,
learning_rate=0.02,
number_training_steps=200):
"""
Instantiate ModelNumberQuestions model and Loss, and optimises the parameters of the model, given the dataset
of tensor_number_tasks and tensor_number_tasks.
Args:
tensor_number_tasks (torch.Tensor): of size (n, 1) where n is the number of questions (it is also the number of tasks)
tensor_number_questions (torch.Tensor): of size (n, 1) where n is the number of questions (it is also the number of tasks)
learning_rate (float):
number_training_steps (int):
Returns:
trained network (ModelNumberQuestions)
"""
net = ModelNumberQuestions() # model
loss = torch.nn.MSELoss() # loss module
optimiser = torch.optim.SGD(net.parameters(), lr=learning_rate)
for _ in range(number_training_steps):
optimiser.zero_grad()
# Compute Loss
estimator_number_questions = net.forward(tensor_number_tasks)
mse_loss = loss.forward(input=estimator_number_questions,
target=tensor_number_questions)
mse_loss.backward()
optimiser.step()
print("loss:", mse_loss.item())
print("Final Parameters:\n", list(net.named_parameters()))
return net
How to execute the code?
def main():
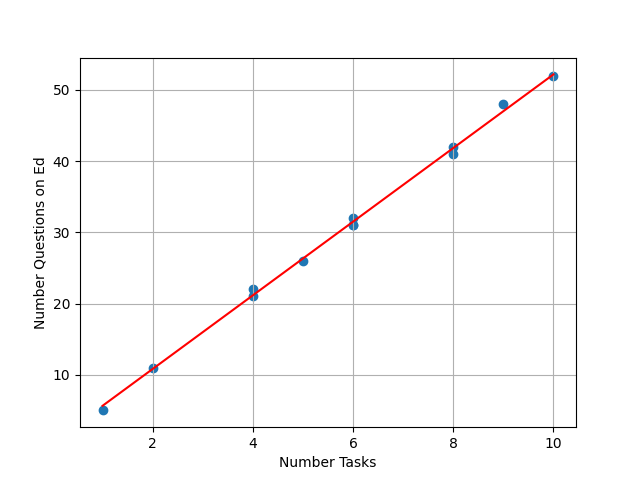
list_number_tasks = [1, 2, 4, 4, 5, 6, 6, 6, 8, 8, 9, 10]
list_number_questions = [5, 11, 21, 22, 26, 31, 32, 31, 41, 42, 48, 52]
tensor_number_tasks = torch.Tensor(list_number_tasks).view(-1, 1)
tensor_number_questions = torch.Tensor(list_number_questions).view(-1, 1)
print(tensor_number_questions)
train_parameters_linear_regression(tensor_number_tasks, tensor_number_questions, learning_rate=0.02, number_training_steps=200)
if __name__ == '__main__':
main()
Code results
The code above produces the following results:
Final Parameters:
[('linear.weight', Parameter containing:
tensor([[5.1577]], requires_grad=True)), ('linear.bias', Parameter containing:
tensor([0.5563], requires_grad=True))]
Which means that our model has learned the following relationship:
\widehat{n_Q} = 5.1577 n_T + 0.5563
where:
- \widehat{n_Q} is an estimator of the number of questions asked on Ed.
- n_T is the number of tasks in the coursework
Those predictions are represented as a red line on the plot below.