Python Programming

The Secrets of torch Parameters.

torch provides very convenient tools to estimate the value of a gradient. The torch Parameter stores the operations applied to it (such as: multiplication, addition, exp…)

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
parameters = torch.nn.Parameter(tensor)
print(parameters)

The code above produces the following output:

Parameter containing:
tensor([[1., 2.],
        [3., 4.]], requires_grad=True)

The requires_grad=True proves that the parameters will keep track of all the operation applied to them, so that the gradients can be computed automatically when needed.

Dynamic Building Graph of Operations

Everytime we perform an operation on a torch Parameter, that operation is recorded in each computed tensor. Those operations are recorded until the loss function.

For example, let’s see what happens after an addition:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
parameters = torch.nn.Parameter(tensor)

temp = parameters + 5
print(temp)

tensor([[6., 7.],
        [8., 9.]], grad_fn=<AddBackward0>)

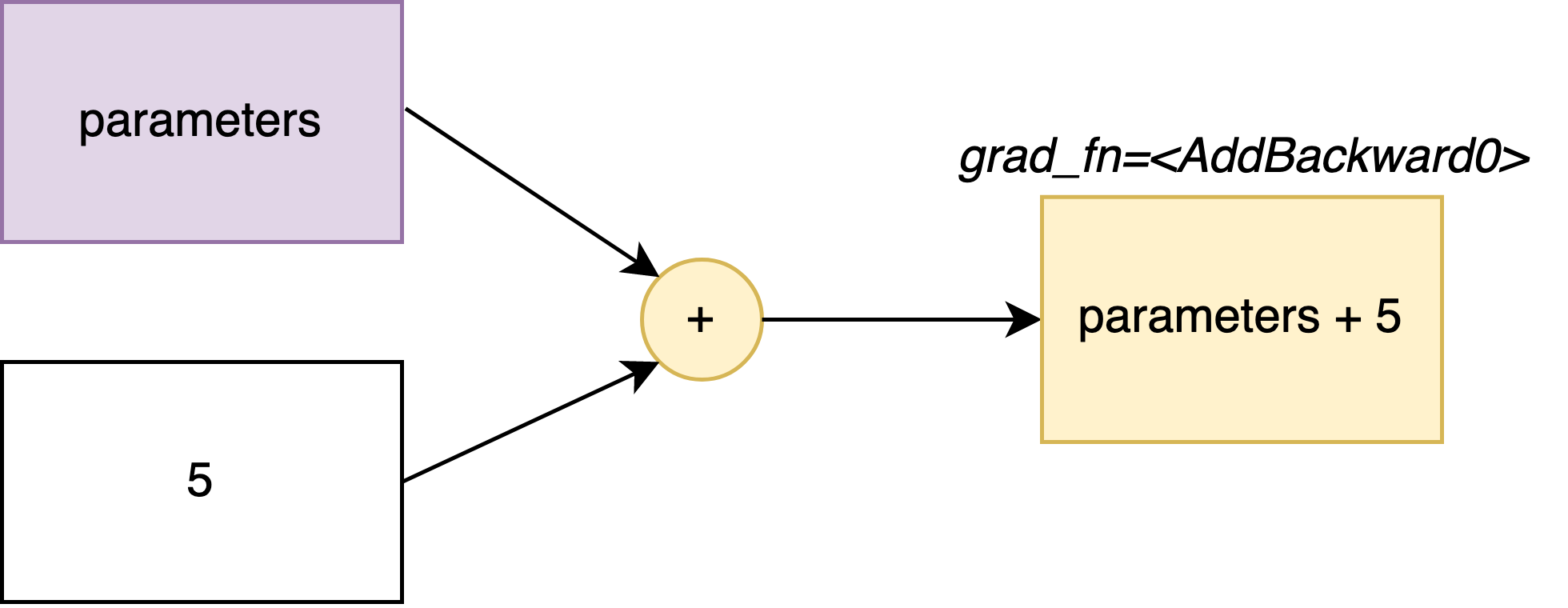
the grad_fn=<AddBackward0> indicates that it remembers the last operation performed on the parameters (in this case: an addition with 5).

The same phenomenon happens with torch mathematical functions, such as torch.exp

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
parameters = torch.nn.Parameter(tensor)

temp = torch.exp(parameters)
print(temp)

tensor([[ 2.7183,  7.3891],
        [20.0855, 54.5982]], grad_fn=<ExpBackward0>)

Automatic Gradients

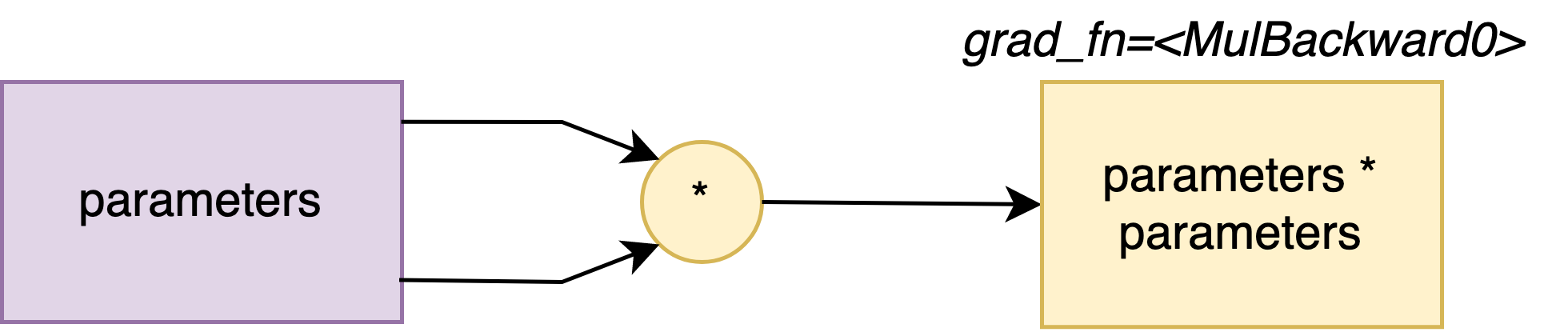
Let’s consider (once again ^^) the squared function $L(\theta) = \theta^2$, and we would like to calculate the gradient $\dfrac{\partial L}{\partial \theta}(\theta_0)$, where $\theta_0 = 1$.

import torch

tensor_0 = torch.Tensor([1])
theta_0 = torch.nn.Parameter(tensor_0)

loss = theta_0 * theta_0
print(loss)

tensor([1.], grad_fn=<MulBackward0>)

grad attribute

Each parameter, including theta_0 presents a grad attribute. Let’s have a look at its value:

print(theta_0.grad)

None

Absolutely no worries! It is completely normal that theta_0.grad equals None right now! We did not tell which gradient we wanted to calculate. :)

Calculating the gradient of the loss.

As said before, we would like to calculate the gradient of the loss $L(\cdot)$ with respect to $\theta$, and evaluate that value at $\theta_0 = 1$: $\dfrac{\partial L}{\partial \theta}(\theta_0)$.

to do so, we simply need to add the following line:

loss.backward()

That method backward() will propagate the gradient of the loss in its computation graph.

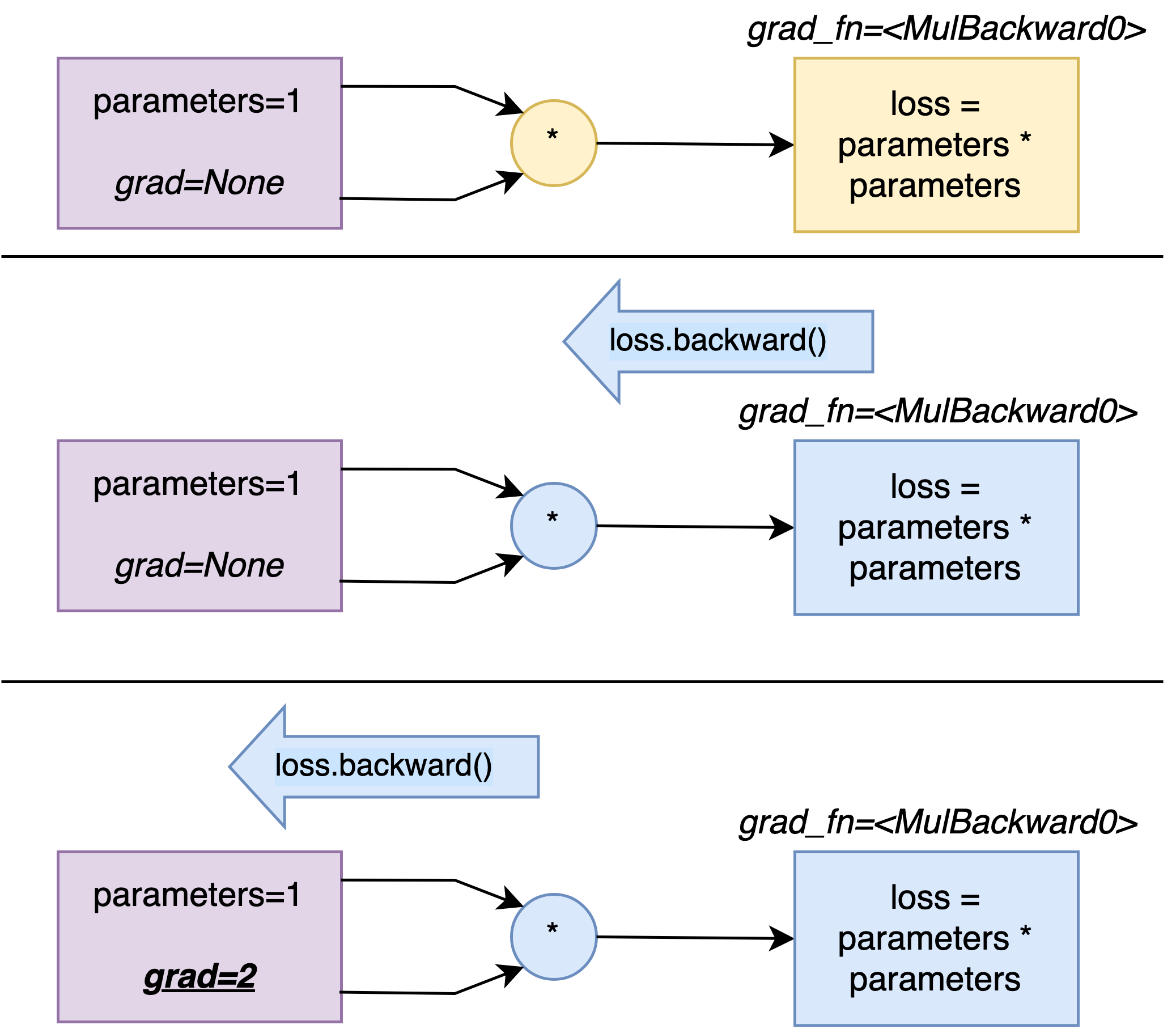
And now if we try to visualise theta_0.grad, we get:

tensor([2.])

which corresponds to the value of $\dfrac{\partial L}{\partial \theta}(\theta_0) = 2\theta_0$ (where $\theta_0 = 1$) .

In other words, now we can compute gradients automatically!