Python Programming

import torch

class ModelNumberQuestions(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = torch.nn.Linear(in_features=1, out_features=1)

    def forward(self, tensor_number_tasks):
        return self.linear(tensor_number_tasks)

def train_parameters_linear_regression(tensor_number_tasks,
                                       tensor_number_questions,
                                       learning_rate=0.02,
                                       number_training_steps=200):
    """
    Instantiate ModelNumberQuestions model and Loss, and optimises the parameters of the model, given the dataset
    of tensor_number_tasks and tensor_number_tasks.

    Args:
        tensor_number_tasks (torch.Tensor): of size (n, 1) where n is the number of questions (it is also the number of tasks)
        tensor_number_questions (torch.Tensor): of size (n, 1) where n is the number of questions (it is also the number of tasks)
        learning_rate (float):
        number_training_steps (int):

    Returns:
        trained network (ModelNumberQuestions)
    """
    net = ModelNumberQuestions()  # model
    loss = torch.nn.MSELoss()  # loss module

    optimiser = torch.optim.SGD(net.parameters(), lr=learning_rate)

    for _ in range(number_training_steps):
        optimiser.zero_grad()

        # Compute Loss
        estimator_number_questions = net.forward(tensor_number_tasks)
        mse_loss = loss.forward(input=estimator_number_questions,
                                target=tensor_number_questions)

        mse_loss.backward()
        optimiser.step()
        print("loss:", mse_loss.item())

    print("Final Parameters:\n", list(net.named_parameters()))
    return net

def main():
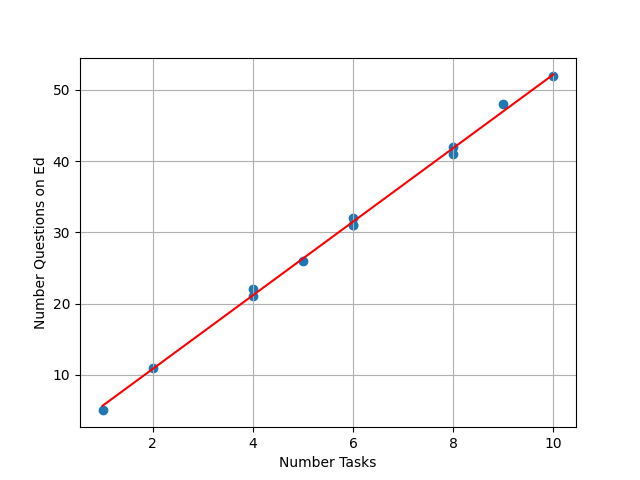
    list_number_tasks = [1, 2, 4, 4, 5, 6, 6, 6, 8, 8, 9, 10]
    list_number_questions = [5, 11, 21, 22, 26, 31, 32, 31, 41, 42, 48, 52]

    tensor_number_tasks = torch.Tensor(list_number_tasks).view(-1, 1)
    tensor_number_questions = torch.Tensor(list_number_questions).view(-1, 1)
    print(tensor_number_questions)
    train_parameters_linear_regression(tensor_number_tasks, tensor_number_questions, learning_rate=0.02, number_training_steps=200)


if __name__ == '__main__':
    main()

Final Parameters:
 [('linear.weight', Parameter containing:
tensor([[5.1577]], requires_grad=True)), ('linear.bias', Parameter containing:
tensor([0.5563], requires_grad=True))]