Introduction to Deep Learning with PyTorch
Chapter 4: PyTorch for Automatic Gradient Descent
Automatic Gradient Calculation with PyTorch
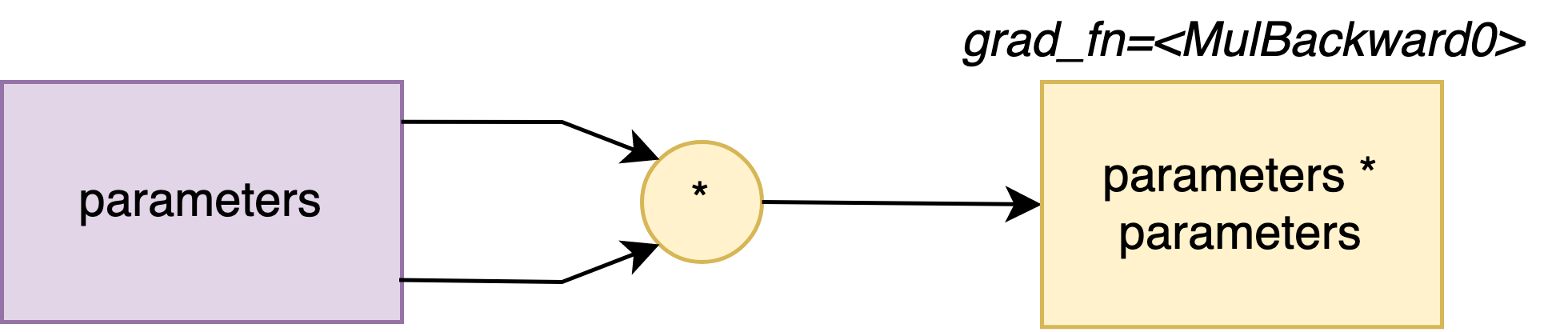
Let’s consider (once again ^^) the squared function L(\theta) = \theta^2, and we would like to calculate the gradient \dfrac{\partial L}{\partial \theta}(\theta_0), where \theta_0 = 1.
import torch
tensor_0 = torch.Tensor([1])
theta_0 = torch.nn.Parameter(tensor_0)
loss = theta_0 * theta_0
print(loss)
tensor([1.], grad_fn=<MulBackward0>)
grad attribute
Each parameter has a grad attribute. Let’s have a look at its value:
print(theta_0.grad)
None
Absolutely no worries!
It is completely normal that theta_0.grad equals None right now!
We did not tell torch which gradient we wanted to calculate. ☺️
Calculating the gradient of the loss
As said before, we would like to calculate the gradient of the loss L(\cdot) with respect to \theta, and evaluate that value at \theta_0 = 1: \dfrac{\partial L}{\partial \theta}(\theta_0).
To do so, we simply need to add the following line:
loss.backward()
The method backward() will propagate the gradient of the loss in its computation graph.
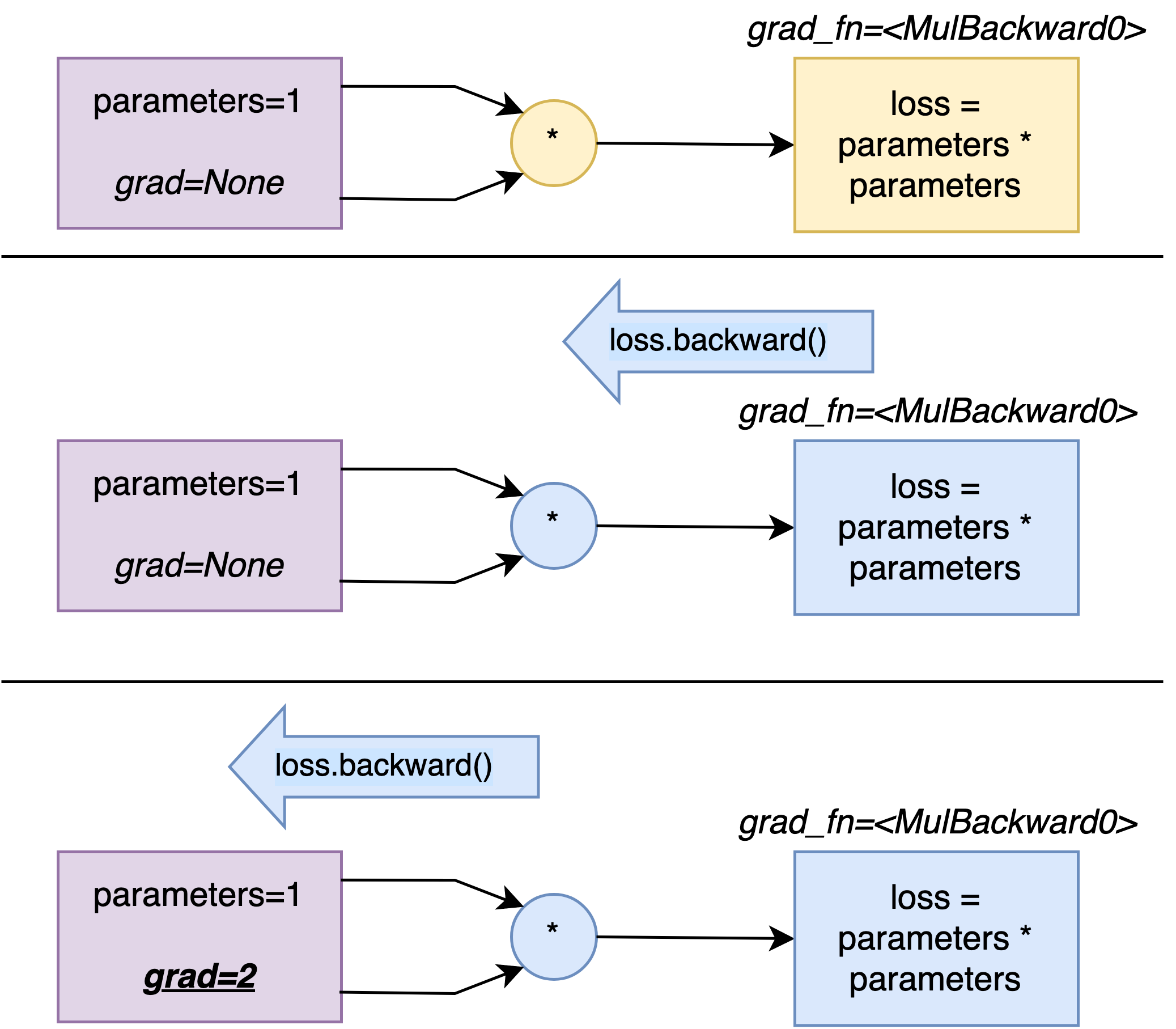
And now if we try to print out theta_0.grad, we get:
tensor([2.])
which corresponds to the value of \dfrac{\partial L}{\partial \theta}(\theta_0) = 2\theta_0 (where \theta_0 = 1) .
In other words, now we can compute gradients automatically!
