Introduction to Deep Learning with PyTorch > Problem Definition | Python Programming (70053 Autumn Term 2022/2023) | Department of Computing

Introduction to Deep Learning with PyTorch

Chapter 5: Training a Linear Model with PyTorch

Problem Definition

face Luca Grillotti

It’s time to train some Machine Learning models to solve some problems.

In this chapter, we’ll focus on a linear regression model to get you started.

Context of the problem

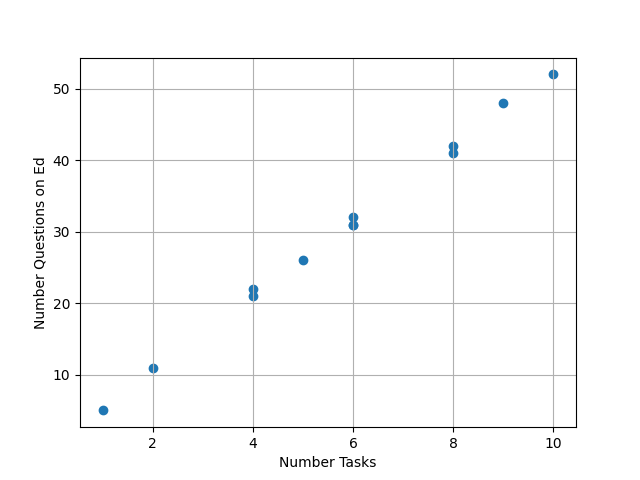
We measured the number of questions asked on ed, depending on the number of tasks present in the specifications:

Data Index	Number of Tasks	Number Questions on Ed
0	1	5
1	2	11
2	4	21
3	4	22
4	5	26
5	6	31
6	6	32
7	6	31
8	8	41
9	8	42
10	9	48
11	10	52

(all those numbers are purely fictitious)

Number Questions asked on Ed per Number of Tasks

Problem Formulation

We would like to build an efficient model $f_\theta(\cdot)$ that predicts an accurate estimator of the number of questions $\widehat{n_Q}$ depending on the number of tasks $n_T$ :

$\widehat{n_Q} = f_\theta(n_T)$

where $\theta$ represents the parameters of our model that we would like to optimise.

Loss Function

We define $n_Q^{(i)}$ as the value of $n_Q$ for the data sample of index $i$ (see table above). For example, $n_Q^{(2)}=19$ and $n_T^{(2)}=4$ .

For each index $i$ , we intend to minimise the squared error between $n_Q$ and its estimation $\widehat{n_Q}$ : $(\widehat{n_Q^{(i)}} - n_Q^{(i)})^2$

In the end, we intend to minimise the mean squared error between all variables $n_Q^{(i)}$ and their estimations $\widehat{n_Q^{(i)}}$ .

$L(\theta) = \dfrac{1}{12} \sum_{i=0}^{11} (\widehat{n_Q^{(i)}} - n_Q^{(i)})^2$

$L(\theta) = \dfrac{1}{12} \sum_{i=0}^{11} (f_\theta(n_T^{(i)}) - n_Q^{(i)})^2$

Chosen Model

We choose to consider here a simple linear model:

$f_\theta(n_T^{(i)}) = \theta_1 n_T^{(i)} + \theta_0$

Thus, the loss we intend to minimise is the following:

$L(\theta) = \dfrac{1}{12} \sum_{i=0}^{11} (\theta_1 n_T^{(i)} + \theta_0 - n_Q^{(i)})^2$

Exercise

You technically already have all the tools to:

compute that loss
automatically perform gradient descent on it

Try to implement a function train_parameters_linear_regression that:

instantiates the parameters theta_0 and theta_1
computes the loss given above
optimises the parameters theta_0 and theta_1 to minimise the loss

def train_parameters_linear_regression(list_number_tasks, list_number_questions, learning_rate=0.02, number_training_steps=200):
    """
    Instantiate ModelNumberQuestions model and optimises the parameters of the model, given the dataset
    of list_number_tasks and list_number_questions.

    Args:
        list_number_tasks (List[float]): of size n where n is the number of questions (it is also the number of tasks)
        list_number_questions (List[float]): of size n where n is the number of questions (it is also the number of tasks)
        learning_rate (float):
        number_training_steps (int):

    Returns:
        trained network (ModelNumberQuestions)
    """

To do so, you can instantiate two torch Parameter:

import torch
initial_theta_0 = torch.Tensor([1])
initial_theta_1 = torch.Tensor([2])
theta_0 = torch.nn.Parameter(initial_theta_0)
theta_1 = torch.nn.Parameter(initial_theta_1)

And here are the dataset lists (corresponding to the table above):

list_number_tasks = [1, 2, 4, 4, 5, 6, 6, 6, 8, 8, 9, 10] # what our model gets as input
list_number_questions = [5, 11, 21, 22, 26, 31, 32, 31, 41, 42, 48, 52] # what we are trying to predict

I’ll let you do the rest 😉

Hint: If your loss function diverges, try lower learning rates.

First let’s declare a function compute_loss

def compute_loss(list_number_tasks, list_number_questions, theta_0, theta_1):
    mse_loss = torch.Tensor([0])

    for number_tasks, number_questions in zip(list_number_tasks, list_number_questions):
        # computing squared error for single data sample (number_tasks, number_questions)
        estimator_number_questions = theta_1 * number_tasks + theta_0
        error = estimator_number_questions - number_questions
        squared_error = error * error

        # adding the computed error to the loss
        mse_loss += squared_error

    # computing mean squared error.
    mse_loss /= len(list_number_tasks)

    return mse_loss

Then, we can use that function in train_parameters_linear_regression to optimise theta_0 and theta_1:

def train_parameters_linear_regression(list_number_tasks, list_number_questions, learning_rate=0.02, number_training_steps=200):
    """
    Instantiate parameters of the model: theta_0 and theta_1.
    And optimises those parameters given the dataset of list_number_tasks and list_number_questions.

    Args:
        list_number_tasks (List[float]): of size n where n is the number of questions (it is also the number of tasks)
        list_number_questions (List[float]): of size n where n is the number of questions (it is also the number of tasks)
        learning_rate (float):
        number_training_steps (int):

    Returns:
        tuple of optimised parameters (Tuple[torch.nn.Parameter, torch.nn.Parameter]) with theta_0 and theta_1
    """

    initial_theta_0 = torch.Tensor([1])
    initial_theta_1 = torch.Tensor([2])
    theta_0 = torch.nn.Parameter(initial_theta_0)
    theta_1 = torch.nn.Parameter(initial_theta_1)

    optimiser = torch.optim.SGD([theta_0, theta_1], lr=learning_rate)

    for _ in range(number_training_steps):
        optimiser.zero_grad()

        mse_loss = compute_loss(list_number_tasks, list_number_questions, theta_0, theta_1)

        mse_loss.backward()  # Compute gradients
        optimiser.step()  # Perform 1-step gradient descent.

        print("loss:", mse_loss.item())

    print(f"theta_0: {theta_0.item()}, theta_1: {theta_1.item()}")

    return theta_0, theta_1