Introduction to Deep Learning with PyTorch > Let's play with tensors! | Python Programming (70053 Autumn Term 2021/2022) | Department of Computing

Introduction to Deep Learning with PyTorch

Chapter 3: PyTorch Tensors

Let's play with tensors!

face Luca Grillotti

Addition and multiplication

With a scalar

Once again, as with numpy arrays, it is easy to add, multiply, subtract and divide by a constant all the components of a tensor:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
tensor_add_item = tensor + 5
tensor_multiply_item = tensor / 2
...
print(tensor_add_item, tensor_multiply_item)

With another tensor

And you can add, multiply, subtract, divide tensors together:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
tensor_add = tensor + tensor
tensor_multiply = tensor * tensor
...
print(tensor_add, tensor_multiply)

Even better, you can easily apply an operation to all the sub-tensors of a tensor. For example:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])
row_tensor = torch.Tensor([1, 2])

tensor_subtract = tensor - row_tensor
print(tensor_subtract)

Other mathematical operations

The torch library provides several mathematical functions that can be applied to all elements of a tensor. For example:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])

tensor_exp = torch.exp(tensor)
tensor_log = torch.log(tensor)
...  # Every single function you could imagine.
print(tensor_exp, tensor_log)

Other statistical operations

There are also plenty of statistical operations available: min, max, mean, … For example:

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4]])

tensor_min = torch.min(tensor)
tensor_max = torch.max(tensor)
tensor_mean = torch.mean(tensor)
...  # Every single mathematical function you could imagine.

print(tensor_min, tensor_max, tensor_mean)

In practice, you will mostly apply those operations on a single axis. For instance, with the tensors above, we could find the minimal element for each row, or for each column.

import torch

tensor = torch.Tensor([[1, 2],
                       [3, 4],
                       [5, 6]])  # shape = (3, 2)

tensor_mean_row = torch.mean(tensor, dim=0)  # shape = (2,) Averaging over 1st dimension (along columns)
tensor_mean_col = torch.mean(tensor, dim=1)  # shape = (3,) Averaging over 2nd dimension (along rows)

print(tensor_mean_row, tensor_mean_col)

Exercise

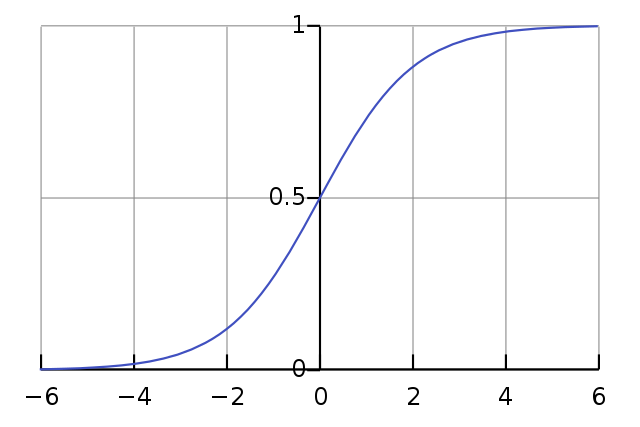
Logistic Function

We define the logistic function $\sigma(\cdot)$ as: $\sigma (x) = \dfrac{1}{1 + e^{-x}}$

This function presents relevant properties:

$\forall x, \: 0 < \sigma (x) < 1$
$\lim_{x \rightarrow -\infty} \sigma (x) = 0$
$\lim_{x \rightarrow +\infty} \sigma (x) = 1$

Those properties make it suitable to model probabilities.

Logistic Curve

Implement a function logistic, applying the above function to all elements of a tensor.

def logistic(tensor):
    """
    Args:
        tensor (torch.Tensor)

    Return:
        logistic_tensor (torch.Tensor) : resulting tensor after having applied the logistic function to all elements of tensor.
    """

def logistic(tensor):
    """
    Args:
        tensor (torch.Tensor)

    Return:
        logistic_tensor (torch.Tensor) : resulting tensor after having applied the logistic function to all elements of tensor.
    """

    return 1 / (1 + torch.exp(-1 * tensor))

Mean of Tensors

Implement a function mean_tensors that takes as input a list of tensors and returns the mean of all those tensors.

def mean_tensors(tensors_list):
    """
    Args:
        tensors_list (List[torch.Tensor]) list of tensors of the same shape

    Return:
        mean_tensors (torch.Tensor) : resulting tensor after having calculated the mean of all tensors passed as input.
    """

One solution would be:

def mean_tensors(tensors_list):
    """
    Args:
        tensors_list (List[torch.Tensor]) list of tensors of the same shape

    Return:
        mean_tensors (torch.Tensor) : resulting tensor after having calculated the mean of all tensors passed as input.
    """
    assert len(tensors_list) > 0
    sum_tensors = tensors_list[0]
    for tensor in tensors_list[1:]:
        sum_tensors += tensor
    mean = sum_tensors / len(tensors_list)
    return mean

Or if you want to be more concise:

def mean_tensors(tensors_list):
    """
    Args:
        tensors_list (List[torch.Tensor]) list of tensors of the same shape

    Return:
        mean_tensors (torch.Tensor) : resulting tensor after having calculated the mean of all tensors passed as input.
    """
    assert len(tensors_list) > 0
    mean = sum(tensors_list) / len(tensors_list)
    return mean

Some other useful methods

`item()`

When we calculated the mean of a tensor, the result was a tensor with a single element:

import torch
tensor = torch.Tensor([[1, 2],
                       [3, 4]])
print(type(tensor.mean()))

However, sometimes, we want to convert the single value present in that tensor into a Python scalar. The item() method is made for that purpose.

import torch
tensor = torch.Tensor([[1, 2],
                       [3, 4]])
mean_item = tensor.mean().item()
print(mean_item,  type(mean_item))

`size()`

If you want to know the shape of a tensor, the size() method (or the shape attribute) is made for you:

import torch

tensor_shape_3_2 = torch.Tensor([[1, 2],
                                 [3, 4],
                                 [5, 6]])  # shape = (3, 2)

print(tensor_shape_3_2.size())
print(tensor_shape_3_2.shape)