Python Programming

Let’s illustrate the main principle of gradient descent in the case of a convex single-variable function:

More specifically, we consider the square function $L : x \rightarrow x^2$. In this case:

• $\dfrac{\partial L}{\partial x} = 2x$.
• $L$ has a global minimum at $x=0$.

And the update rule is:

$x \leftarrow x - \lambda \dfrac{\partial L}{\partial x}$

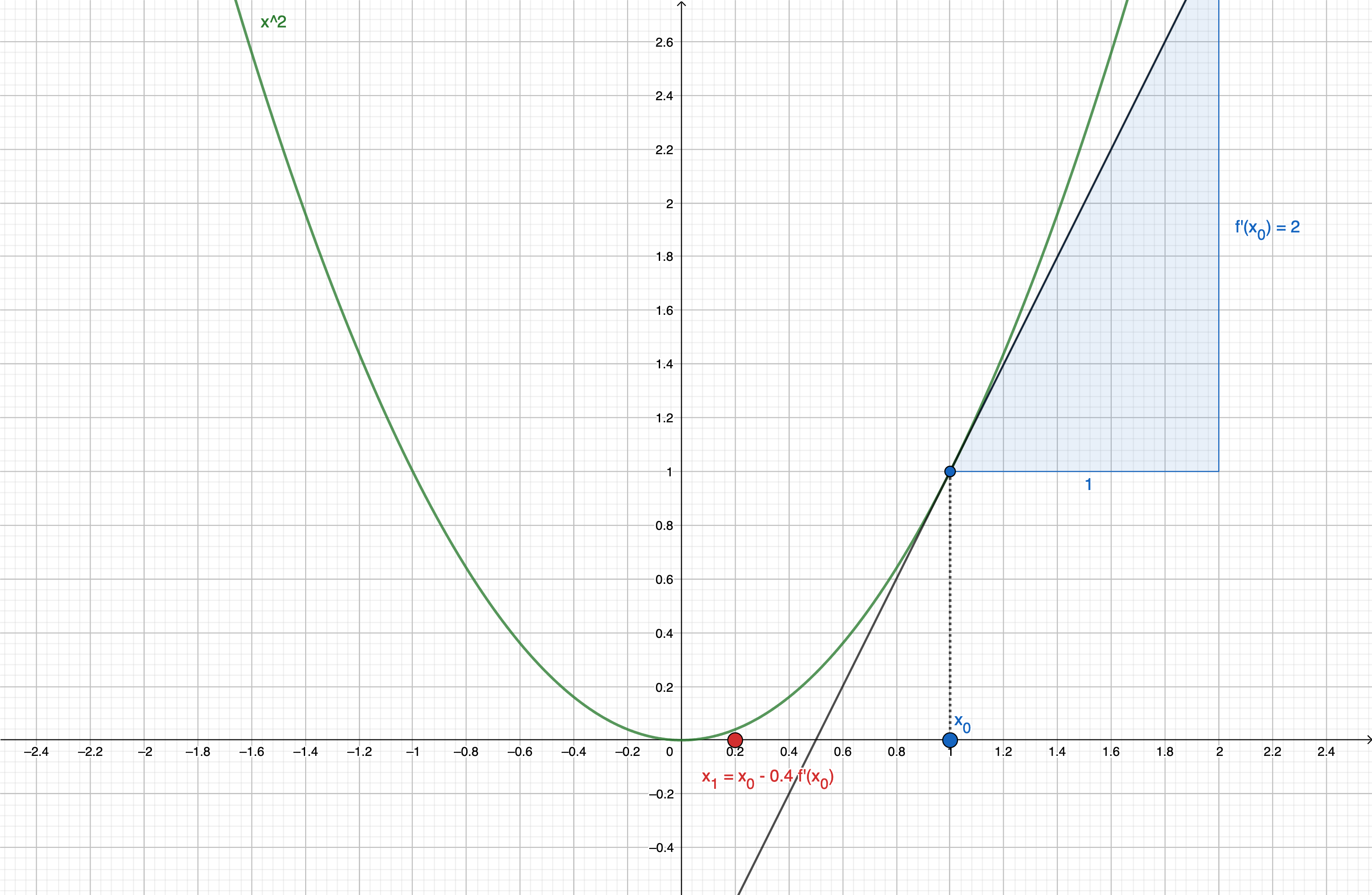
x > 0

We take $x_0 = 1$.

As $x_0>0$, $\dfrac{\partial L}{\partial x}(x_0) > 0$.

So, as $x_1 \leftarrow x_0 - \lambda \dfrac{\partial L}{\partial x}(x_0)$:

• $x_1 < x_0$
• if $\lambda$ is small enough, $x_1$ will be closer to 0. (see figure below, for $\lambda=0.4$ )

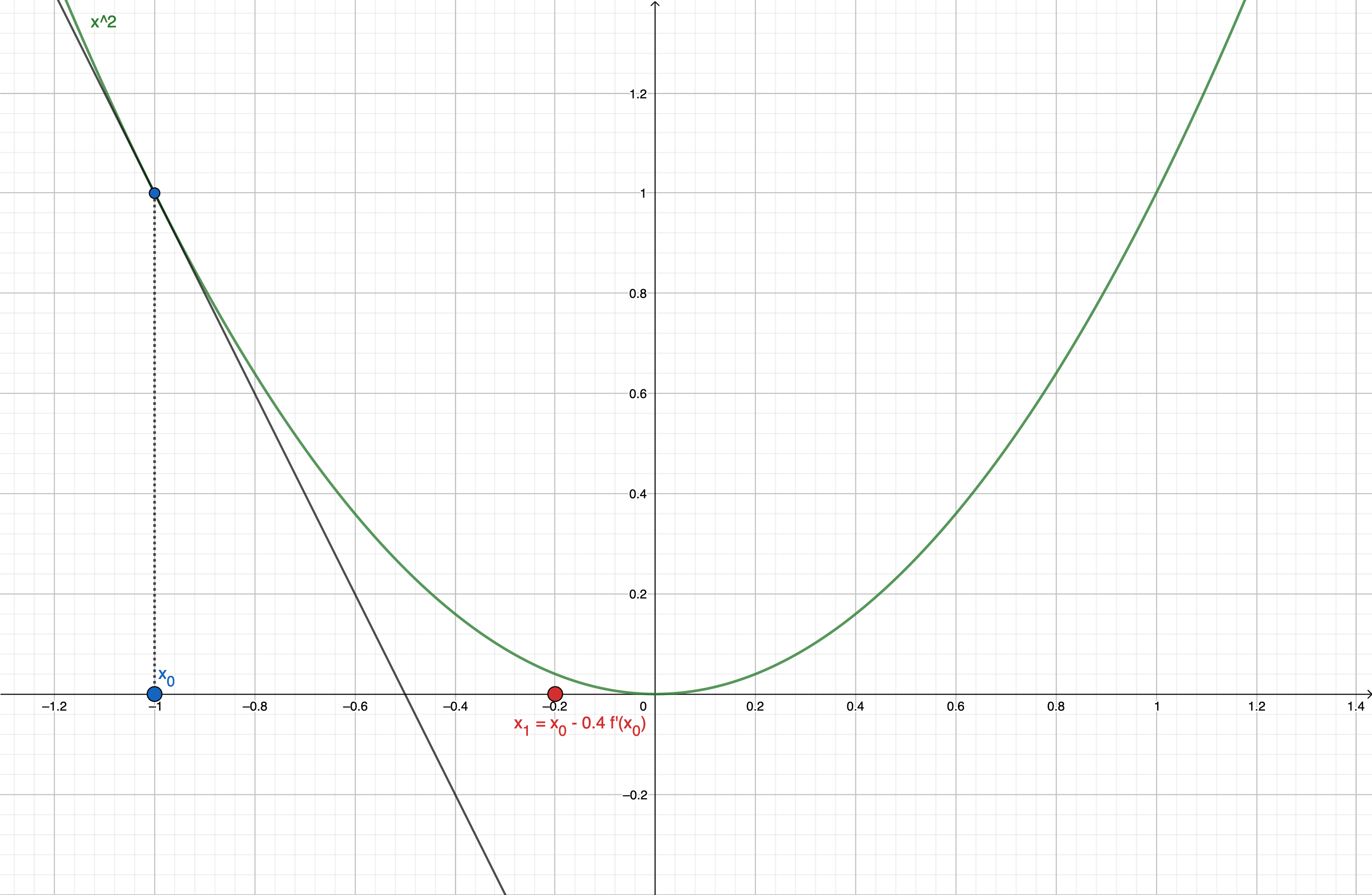
x < 0

We take $x_0 = -1$.

As $x_0<0$, $\dfrac{\partial L}{\partial x}(x_0) < 0$.

So, as $x_1 \leftarrow x_0 - \lambda \dfrac{\partial L}{\partial x}(x_0)$:

• $x_1 > x_0$
• if $\lambda$ is small enough, $x_1$ will be closer to 0. (see figure below, for $\lambda=0.4$ )