Lesson 7
Objects and Dictionaries
Chapter 6: Recursion
Summary on recursion
Hopefully you now know that recursion can be a powerful alternative to while/for loops to implement repetition!
I have only presented simple examples for recursion in this chapter to illustrate the concept. In fact, these examples are probably more efficiently implemented using loops!
But there are times when using recursion is more elegant and readable (and perhaps easier to write). It might sometimes provide a higher level of abstraction over using loops. Think of how self-explanatory the recursive versions of factorial and Fibonacci are!
Recursion is an example of a divide-and-conquer paradigm (we touched on this briefly when discussing composition and abstraction). You break down tasks into smaller subproblems, and the solutions to the smaller subproblems can then be combined to solve the bigger problem.
Start noticing recursions in different problems! For example, you can check for palindromes using recursion (assuming we did not have a convenient way to reverse a string)
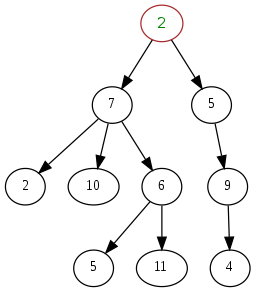
A tree data structure is the best example use case for recursion. These are often used in search and sorting algorithms. You can elegantly navigate down a tree to its children nodes using recursion (say from node 2 down to node 11 in the figure below). Recursive functions will help break down this complex task into simpler sub-problems. So you navigate down to a child, and the child will navigate down to its child, etc. Imagine having to write complicated nested loops to do this, especially when you do not know in advance how many branches or how deep the tree is! In fact, if you are taking the Introduction to Machine Learning module, you will be implementing a decision tree from scratch in your coursework! You’ll need recursion for that! 🌲
We will not have time to practice more recursion (you still have a lot of cover!) In any case, hopefully you get the whole concept of recursion. Remember that using recursion often requires a “leap of faith”! If you have thought and defined the base and recursive cases carefully, you should then trust that your recursive functions will do the right thing!
